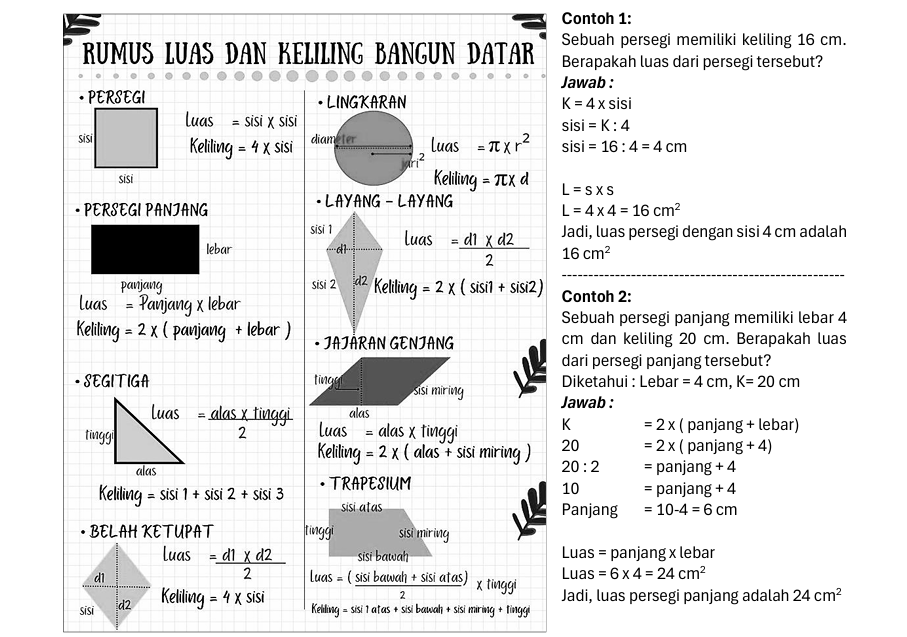
Menentukan Luas Bangun Datar dari Keliling yang Diketahui

1. Persegi

Rumus Keliling: K = 4 × s

Rumus Luas: L = s²

Contoh: Jika keliling 40 cm, maka s = 10 cm. Luas = 100 cm²

2. Persegi Panjang

Rumus Keliling: K = 2 × (p + l)

Rumus Luas: L = p × l

Contoh: K = 30 cm, p = 8 → l = 7. Luas = 56 cm²

3. Segitiga Sama Sisi

Keliling: K = 3 × s

Luas: L = ½ × a × t

Contoh: K = 18 → s = 6. Luas ≈ 15.6 cm²

4. Lingkaran

Keliling: K = 2 × π × r

Luas: L = π × r²

Contoh: K = 31.4 → r = 5. Luas = 78.5 cm²

5. Trapesium

Keliling: jumlah semua sisi

Luas: L = ½ × (a + b) × t

Contoh: K = 30, sisi diketahui → Luas = 45 cm²

6. Jajar Genjang

Keliling: K = 2 × (a + b)

Luas: L = a × t

Contoh: K = 36, a = 10 → b = 8 → Luas = 40 cm²

7. Belah Ketupat

Keliling: K = 4 × s

Luas: L = ½ × d₁ × d₂

Contoh: K = 40 → s = 10, d₁ = 12 → d₂ ≈ 16 → Luas = 96 cm²

8. Layang-Layang

Keliling: 2 × (a + b)

Luas: L = ½ × d₁ × d₂

Contoh: K = 48, a = 10, b = 14, d₁ = 12 → d₂ ≈ 25.3 → Luas ≈ 151.8 cm²

Kesimpulan

Dengan memahami dan menguasai rumus serta hubungan antar parameter bangun datar, peserta didik dapat menentukan luas berdasarkan informasi keliling yang diberikan. Praktik secara rutin akan memperkuat keterampilan ini dalam kehidupan nyata maupun ujian sekolah.