Kunci Jawaban Matematika Kelas 8 Halaman 167
gurune.net – Kunci Jawaban Matematika Kelas 8 Halaman 167 . Halo sobat guru! Kali ini gurune akan membahas kunci jawaban matematika kelas 8.
Pada kelas 8, sobat guru akan belajar persamaan garis. Soal latihan yang akan kita bahas kali ini bisa sobat guru temukan pada buku matematika kelas 8 semester 1 halaman 167 kurikulum 2013.
Sebelum membaca jawaban berikut, alangkah baiknya jika sobat guru mencoba mengerjakan sendiri terlebih dahulu. Kemudian cocokan jawaban yang sudah sobat guru tulis dengan jawaban dari gurune.
Kunci Jawaban Matematika Kelas 8 Halaman 167
1. Tulislah persamaan garis yang ditunjukkan tiap-tiap gambar berikut.
Jawaban :
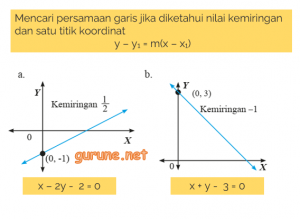
2. Tulislah persamaan garis yang ditunjukkan tiap-tiap gambar berikut
Jawaban :

3. Tulislah persamaan garis yang sesuai pada tiap-tiap gambar berikut
Jawaban :

4. Tentukan persamaan garis lurus jika kita ketahui informasi berikut ini.
Jawaban :

5. Tentukan persamaan garis yang melalui (7, 2) dan sejajar dengan garis 2x – 5y = 8
Jawaban :

Simak pembahasan nomor 6-10 di link ini
Penutup
Nah sobat guru, demikian jawaban Matematika Kelas 8 yang bisa gurune bagikan. Semoga Bermanfaat.
Disclaimer:
1. Jawaban dan pembahasan pada postingan ini mungkin akan berbeda dengan jawaban atau contoh yang oleh Bapak/Ibu Guru berikan di sekolah.
2. Jadikan postingan ini sebagai salah satu bahan referensi dalam menjawab soal bukan sebagai acuan utama dan satu-satunya
3. Postingan ini tidak mutlak kebenarannya.


