Menghitung Volume Bangun Ruang dari Kubus Satuan: Strategi Jitu untuk Peserta Didik

Menghitung Volume Bangun Ruang dari Kubus Satuan: Strategi Jitu untuk Peserta Didik – Disajikan gambar bangun ruang yang terdiri dari susunan kubus satuan peserta didik dapat menentukan volume bangun ruang tersebut dengan benar—kalimat ini sering muncul dalam soal-soal matematika tingkat dasar hingga menengah. Tak hanya menjadi bahan ujian, kemampuan ini juga penting sebagai dasar logika spasial dan numerik anak. Sayangnya, masih banyak peserta didik yang kebingungan ketika dihadapkan pada soal semacam ini.

Dalam artikel ini, kita akan mengulas tuntas cara menentukan volume bangun ruang dari susunan kubus satuan. Mulai dari pengertian dasar, metode penghitungan, hingga strategi cerdas agar peserta didik tak mudah terkecoh oleh gambar yang tampak rumit.

Memahami Konsep Dasar Volume Bangun Ruang

Sebelum kita membedah satu per satu gambar bangun ruang, ada baiknya kita pahami terlebih dahulu apa yang dimaksud dengan volume dan bagaimana cara menghitungnya. Volume adalah ukuran ruang tiga dimensi yang ditempati oleh suatu objek. Dalam konteks ini, objek tersebut adalah bangun ruang yang tersusun dari kubus satuan, yaitu kubus dengan panjang rusuk satuan (1 satuan panjang).

Jika satu kubus satuan memiliki volume 1 satuan kubik, maka bangun ruang yang terdiri dari 5 kubus satuan akan memiliki volume sebesar 5 satuan kubik. Terdengar mudah? Ya, secara teori memang begitu. Tapi ketika bentuk bangunnya tidak simetris atau tumpukan kubus tidak terlihat jelas, peserta didik sering kali terkecoh.

Mengapa Penting Memahami Volume dari Kubus Satuan?

Kemampuan menghitung volume dari susunan kubus bukan hanya soal matematika semata. Ini berkaitan erat dengan pengembangan kecerdasan spasial, kemampuan visualisasi tiga dimensi, serta logika numerik. Anak yang terbiasa melatih kemampuan ini akan lebih mudah memahami konsep geometri lanjut, teknik konstruksi, hingga pemrograman komputer yang berbasis logika spasial.

Lebih dari itu, pemahaman terhadap konsep volume juga dibutuhkan dalam kehidupan sehari-hari, seperti saat mengisi air ke dalam bak, memperkirakan jumlah kotak dalam tumpukan barang, atau bahkan saat mendesain ruangan.

Strategi Menentukan Volume dari Gambar Susunan Kubus

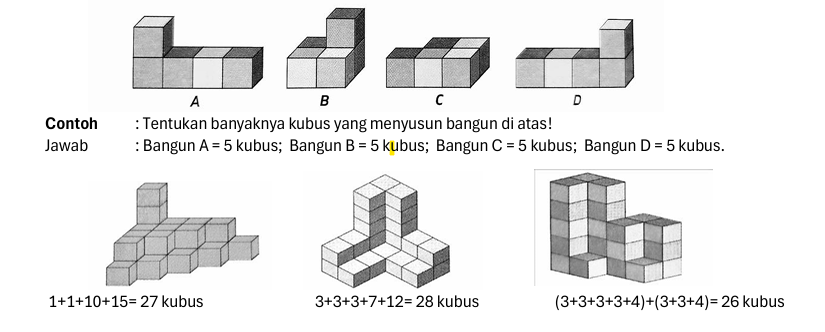
Mari kita bahas lebih rinci soal-soal bergambar seperti yang terdapat dalam gambar di atas. Gambar ini menyajikan beberapa bangun ruang unik yang terdiri dari tumpukan kubus satuan, baik dalam posisi datar, bertingkat, maupun dalam susunan kompleks.

1. Menghitung Jumlah Kubus dengan Cermat

Langkah pertama adalah menghitung seluruh jumlah kubus yang menyusun bangun ruang. Ini bisa dilakukan dengan metode:

• Menghitung dari lapisan bawah ke atas

• Mengelompokkan berdasarkan kolom

• Memvisualisasikan bagian yang tidak terlihat

Misalnya, pada bangun pertama (kiri bawah), kita dapat membagi bangun menjadi beberapa lapisan. Lapisan pertama terdiri dari 15 kubus, lapisan kedua 10 kubus, lapisan ketiga 1 kubus, dan lapisan keempat 1 kubus. Totalnya: 1 + 1 + 10 + 15 = 27 kubus.

2. Mewaspadai Kubus yang Tersembunyi

Gambar dua dimensi kadang tidak menampilkan kubus yang tersembunyi di balik kubus lain. Peserta didik perlu membayangkan bentuk tiga dimensi secara utuh, dan memperkirakan berapa banyak kubus yang berada di belakang atau di bawah.

Bangun tengah (tengah bawah) adalah contoh klasik. Meskipun hanya terlihat 16 kubus di depan, sebenarnya jumlah totalnya mencapai 28 kubus, karena tumpukan-tumpukan yang tidak terlihat dari depan bisa dihitung secara sistematis.

3. Menggunakan Warna atau Arsiran (Jika Disediakan)

Beberapa soal menyertakan arsiran atau warna berbeda untuk membedakan lapisan. Ini bisa dimanfaatkan untuk mengidentifikasi level dan jumlah kubus dengan lebih akurat. Namun, jika tidak disediakan, peserta didik perlu mengandalkan ketelitian dan latihan visualisasi.

Latihan-Latihan Populer: Memecahkan Gambar yang Sulit

Berikut beberapa latihan yang sering muncul dalam soal UN, AKM, atau ujian harian:

Latihan 1: Bangun Ruang Bertingkat

Bangun terdiri dari susunan horizontal 3×3, lalu di atasnya ada susunan 2×2, dan satu kubus tunggal di puncak.

Strategi:

• Lapisan pertama: 9 kubus

• Lapisan kedua: 4 kubus

• Lapisan ketiga: 1 kubus

Total volume: 9 + 4 + 1 = 14 satuan kubik

Latihan 2: Tumpukan Diagonal

Kubus ditumpuk menyerupai tangga dari kiri ke kanan.

Strategi:

• Hitung setiap kolom secara vertikal

• Kolom 1: 3 kubus

• Kolom 2: 2 kubus

• Kolom 3: 1 kubus

Total volume: 3 + 2 + 1 = 6 satuan kubik

Cara Membiasakan Peserta Didik Agar Terampil

Agar siswa bisa menentukan volume bangun ruang dari susunan kubus satuan dengan benar, ada beberapa strategi pembelajaran yang bisa diterapkan oleh guru:

1. Latihan dengan Balok Nyata

Gunakan media konkret seperti balok mainan atau lego agar siswa bisa menyentuh dan melihat bentuk tiga dimensi secara langsung.

2. Gambar Isometrik

Latih siswa menggambar bangun ruang dari berbagai sudut pandang. Ini membantu mereka membayangkan bagian-bagian yang tersembunyi.

3. Diskusi Visualisasi

Ajarkan siswa untuk menyebutkan jumlah kubus secara verbal sembari menunjuk bagian bangun. Hal ini membantu mereka mengingat dan mengasah kemampuan spasial.

4. Permainan Edukatif

Permainan seperti Minecraft atau permainan konstruksi lain bisa menjadi sarana melatih logika tiga dimensi siswa secara menyenangkan.

Kesalahan Umum yang Harus Dihindari

Beberapa kesalahan yang sering dilakukan siswa antara lain:

• Mengabaikan kubus yang tersembunyi

• Menganggap semua sisi terlihat adalah jumlah total

• Menghitung dua kali bagian yang sama

• Lupa membedakan antara panjang, lebar, dan tinggi

Untuk itu, penting untuk terus melatih kejelian dan ketelitian saat melihat gambar bangun ruang.

Kesimpulan

Menentukan volume bangun ruang dari susunan kubus satuan bukanlah soal yang sulit jika siswa memahami konsep dan memiliki strategi penghitungan yang tepat. Dengan memahami bahwa setiap kubus satuan bernilai 1 satuan kubik, serta mampu memvisualisasikan bagian tersembunyi dari gambar, siswa akan semakin percaya diri menjawab soal semacam ini.

Kunci keberhasilan terletak pada latihan berulang, penggunaan media konkret, serta kemampuan guru dalam memandu diskusi visualisasi tiga dimensi. Dalam ujian, pemahaman ini akan sangat membantu, tak hanya dalam matematika, tapi juga dalam bidang lain seperti sains, teknologi, bahkan seni desain.

Jadi, bila disajikan gambar bangun ruang yang terdiri dari susunan kubus satuan, peserta didik seharusnya dapat menentukan volume bangun ruang tersebut dengan benar—dan bahkan lebih dari itu, mampu menjelaskannya dengan logis dan runtut.